autostats • autostats

library(autostats)

plot variable contributions

multiclass target

Species is a 3-level factor so it will be automatically modelled with a multiclass neural network and a light gbm with multiclass objective function.

First set define the formula to use for modeling.

iris %>% 
  tidy_formula(target = Species) -> species_formula

species_formula
#> Species ~ Sepal.Length + Sepal.Width + Petal.Length + Petal.Width
#> <environment: 0x1293e6db8>

iris %>% 
  auto_variable_contributions(species_formula)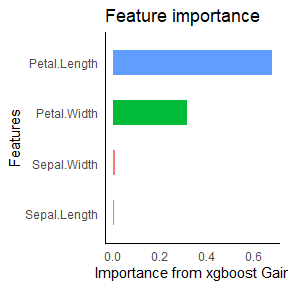

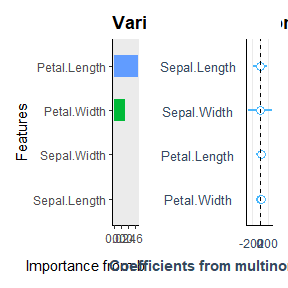
iris %>% 
  auto_model_accuracy(species_formula)

4 - fold cross-validated accuracy for classification model of Species on dataset iris
model	metric	mean_score	std_err
xgboost	accuracy	0.960	0.01363
	brier_class	0.035	0.01288
	roc_auc	0.995	0.00406

binary target

Linear models uses weighted logistic regression for modeling the coefficients

iris %>% 
  filter(Species != "setosa") %>% 
  auto_variable_contributions(species_formula)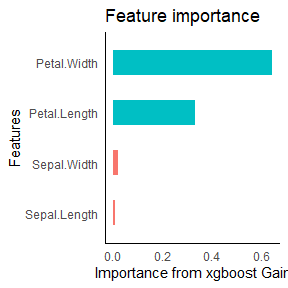

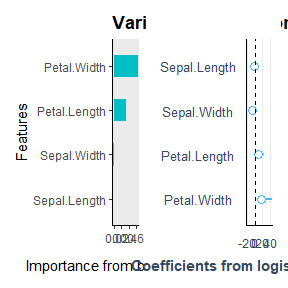
For the variable contributions the linear model uses penalized logistic regression provided by glmnet.

iris %>% 
  filter(Species != "setosa") -> iris_binary

iris_binary %>% 
  auto_model_accuracy(species_formula)

4 - fold cross-validated accuracy for classification model of Species on dataset iris_binary
model	metric	mean_score	std_err
xgboost	accuracy	0.9200	0.0490
	brier_class	0.0646	0.0384
	roc_auc	0.9800	0.0200

continuous target

Models are automatically adapted for a continuous target.

Define the new formula

iris %>% 
  tidy_formula(target = Petal.Length) -> petal_formula

petal_formula
#> Petal.Length ~ Sepal.Length + Sepal.Width + Petal.Width + Species
#> <environment: 0x1396fb7c8>

iris %>% 
  auto_model_accuracy(petal_formula)

4 - fold cross-validated accuracy for regression model of Petal.Length on dataset iris
model	metric	mean_score	std_err
xgboost	rmse	0.279	0.01256
xgboost	rsq	0.974	0.00262

auto anova

auto anova automatically regresses each continuous variable supplied against each categorical variable supplied. Lm is called separately for each continuous/ categorical variable pair, but the results are reported in one dataframe. Whether the outcome differs amongst categorical levels is determined by the p.value. The interpretation is affected by the choice of baseline for comparison. Traditionally the first level of the factor is used, however option to use the mean of the continuous variable as the baseline intercept is a helpful comparison.

iris %>% 
  auto_anova(Species, matches("Petal"), baseline = "first_level")
#> # A tibble: 6 × 12
#>   target      predictor level estimate target_mean     n std.error level_p.value
#>   <chr>       <chr>     <chr>    <dbl>       <dbl> <int>     <dbl>         <dbl>
#> 1 Petal.Leng… Species   (Int…    1.46        1.46     50    0.0609      9.30e-53
#> 2 Petal.Leng… Species   vers…    2.80        4.26     50    0.0861      5.25e-69
#> 3 Petal.Leng… Species   virg…    4.09        5.55     50    0.0861      4.11e-91
#> 4 Petal.Width Species   (Int…    0.246       0.246    50    0.0289      1.96e-14
#> 5 Petal.Width Species   vers…    1.08        1.33     50    0.0409      1.25e-57
#> 6 Petal.Width Species   virg…    1.78        2.03     50    0.0409      7.95e-86
#> # ℹ 4 more variables: level_significance <chr>, predictor_p.value <dbl>,
#> #   predictor_significance <chr>, conclusion <chr>